Ut Queant Laxis
<=>
Dans cette énigme, il faudra faire à nouveau intervenir la musique
<=>
On traduit par : A CARIGNAN
Pour trouver la spirale à quatre centres,
560 606 mesures, c'est loin.
Mais par le méga, c'est un million de fois moins
<=>
Patience aussi pour comprendre cette partie
Les 560 606 mesures représentent 185k ( 560 606 x 0,33 m = 185 000 m )
Il nous faut reporter avec précision nos trouvailles sur la carte au 1/1 000 000°.
<=>
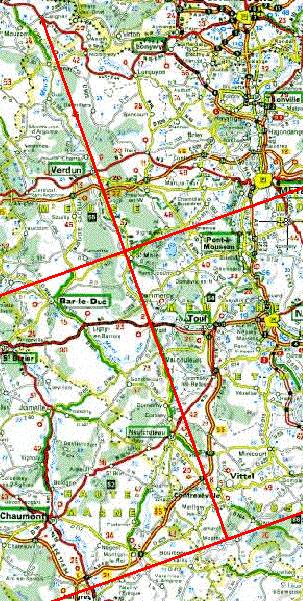
Ensuite, on voit la règle qui montre comment compter les 18,5 cm... Ils se comptent sur l'orthogonale par rapport à la portée depuis Carignan.
La ligne Forbach-Angers est notre ligne de FA. On se rappelle que la
clé est une clé de main gauche ( en 600 ) sur le visuel, on voit une
clé de sol.
Il s'agira donc de transposer la ligne FA dans une autre clé.
<=>
On trace ensuite la parallèle à Forbach-Angers située au bout de ces 18,5 cm
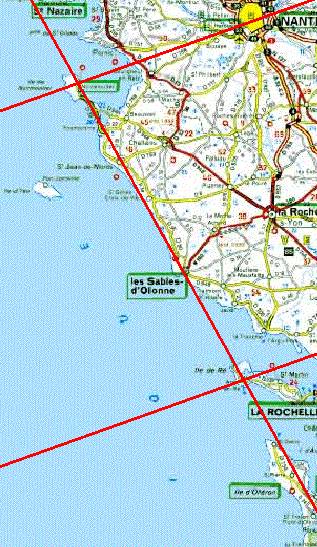
<=>
Pourquoi Ré ?
La clé de fa est située sur la troisième ligne. Si on change la clé,
Fa devient Ré.
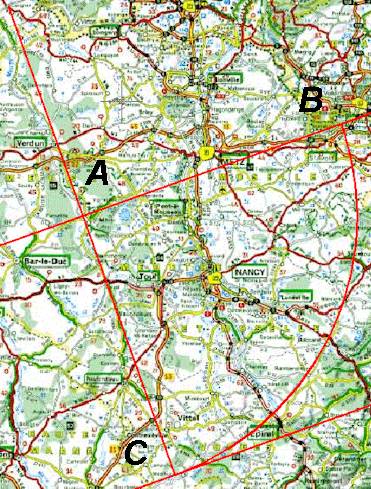
On reporte ( Compas à pointes sèches ) la distance [AC] sur la droite (FA). On arrive à Forbach ( F = FA ). A nouveau, on retrouve une spirale à quatre centres.
On en conclue, avec un peu de malice, qu'il y a 2 portées à tracer. Une, dans le sens donnée par Forbach-Angers et l'autre perpendiculaire à cette droite.
Une fois les deux portées tracées, il m'a paru logique de continuer le quadrillage. Le résultat, même s'il sort de la carte ( mais rien ne l'interdit ) est intéressant car il couvre parfaitement la carte.
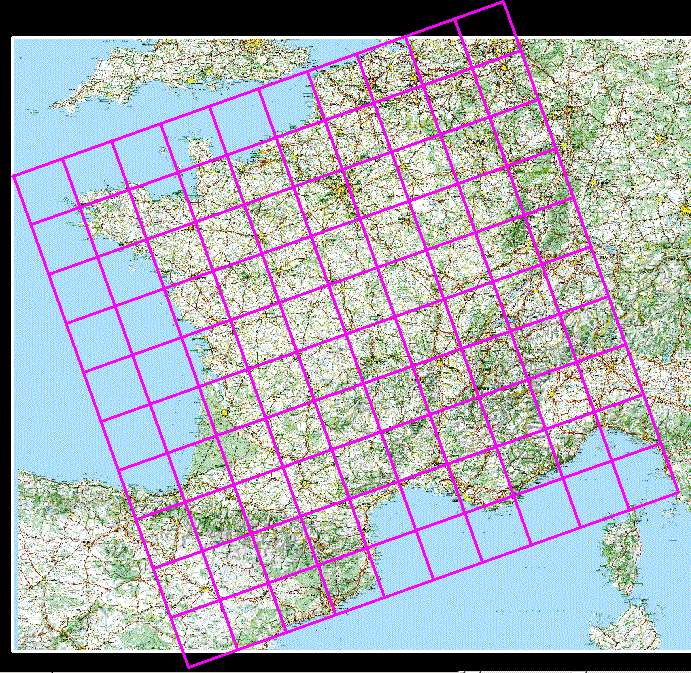
Vous ne pouvez pas le voir, la carte à cette taille est trop
imprécise, mais le haut du damier est a 2 ou 3 mm du nord du Pas de
Calais et le trait droit passe a 2 ou 3 mm du coin est de la frontière.
Par ailleurs, il n'est pas possible, avec cette orientation de départ et
cette taille de case de faire moins que 10x10 cases. On oublierait les
îles d'Ouessant à l'ouest ou le bas de la côte méditerranée au sud.